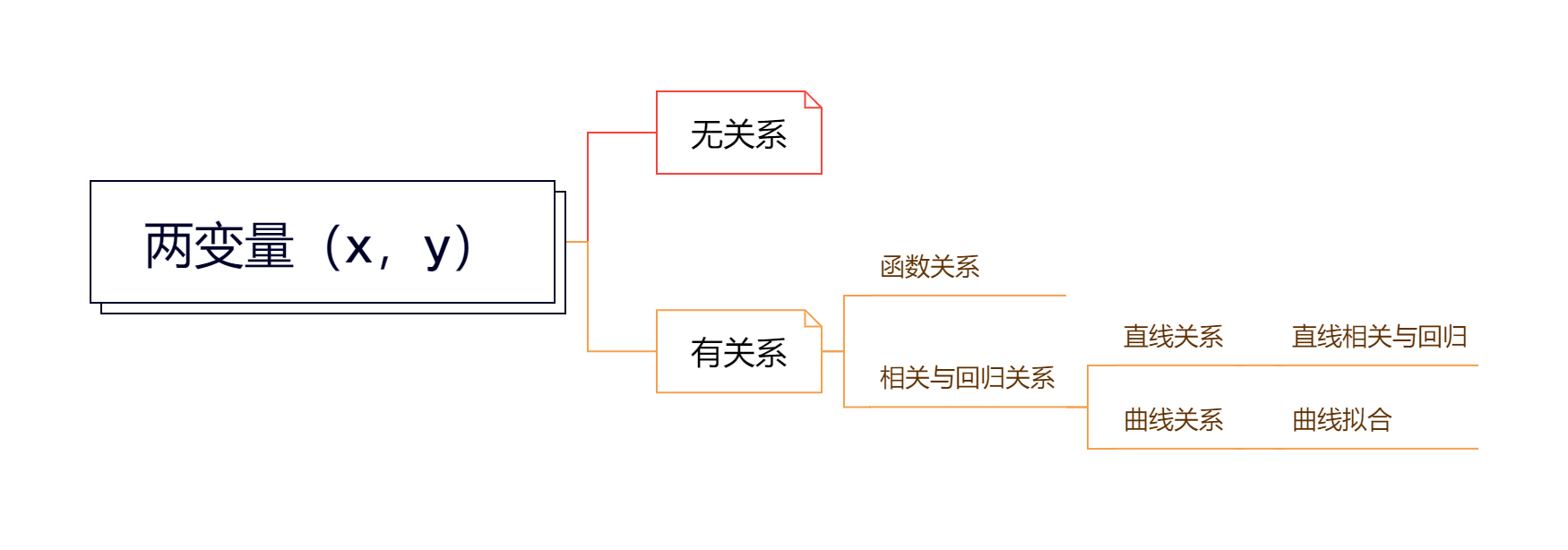
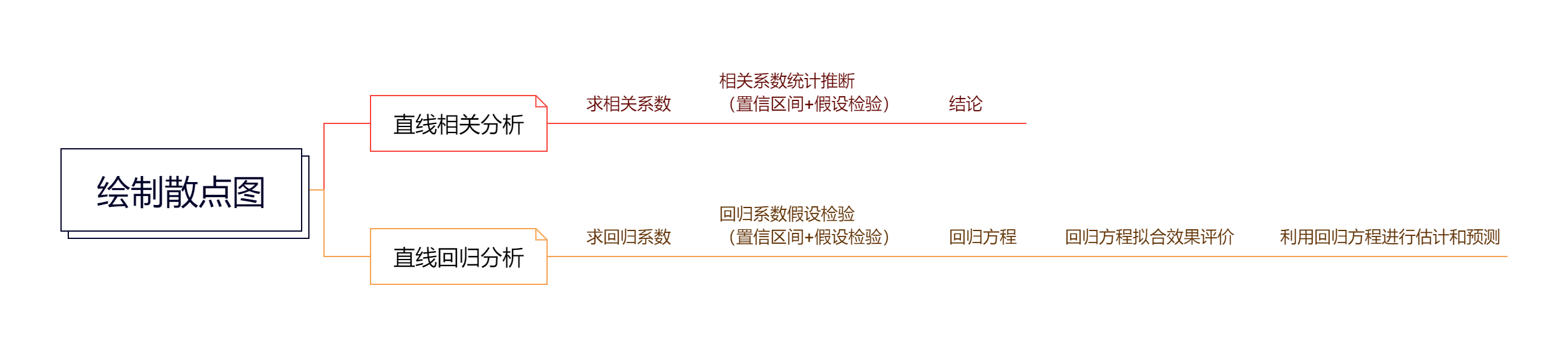
--- title: "简单线性相关和回归" author: "Simonzhou" date: "2025-02-27" #format: # html: # 输出格式为 HTML # self-contained: true # 生成独立的 HTML 文件 # pdf: # 可选:如果需要 PDF 输出 # default execute: echo: true # 在输出中显示代码 eval: true # 执行代码 warning: false # 隐藏警告信息 message: false # 隐藏消息 cache: true # 启用代码缓存 freeze: true # 冻结代码输出 --- # 简单线性相关和回归 ## 两变量关系分析  ## 常见相关系数 ### 直线相关分析基本流程  ### 三类相关系数总结 # 简单直线回归 ### 直线回归分析的基本流程  ### 回归方程的建立 \\ \\ ## 假设检验 ### F检验 \\ [ a + bx_i - (a + b\bar x) ] ^2 \\ \\ \\ \\ ### t检验法 ## 直线回归方程的区间估计 ### 总体回归系数的置信区间 ## 直线相关与直线回归的比较 \. <font color=Red>线性相关</font>要求X,Y服从<font color=Red>双变量正态分布</font>,对这种资料进行回归分析称为$\textrm{II}$型回归,即可以把X当自变量,也可以当因变量,反之亦然。<br>2. <font color=Red>线性回归要求<font color=Red>Y在给定X值时服从正态分布</font>,X可以是精确测量和严格控制的变量,这时的回归称为\textrm{I}型回归,即不可以把X当因变量,Y当自变量进行回归分析。 |\. <font color=Red>线性相关用来表达两个变量间的互依关系</font>,两个变量的研究<font color=Red>地位是相等的</font>,谁做X,谁做Y都可以;<br>2. <font color=Red>线性回归用来表达两个变量间的依存变化的数量关系</font>,即一个变量(为因变量Y)如何依存于另一个变量(为自变量X)而变化,两个变量的研究<font color=Red>地位是不相等的</font>。 |\. 相关系数r说明具有线性关系的两个变量之间的<font color=Red>密切程度和相关方向</font>;<br>2. 回归系数b表示X每变化一个单位所导致的<font color=Red>Y的平均变化量</font>。 |[ 0,1 ] $当总平方和的大小决定了相关的密切程度,回归平方和越接近总平方和,则$R^2$越接近1,相关的效果越好,说明回归效果越好,相关的密切程度也越高。 |# **notice**:关于双变量正态分布 ## 数学定义 \\ \\ ## 性质 - 边缘分布:$X$ 和 $Y$ 的边缘分布也是正态分布。- 条件分布:给定 $X$ 的值,$Y$ 的条件分布也是正态分布。- 相关性:协方差矩阵的值可以用来判断 X 和 Y 之间的相关性。如果 $\sigma_{XY} > 0$,则两者正相关;如果 $\sigma_{XY} < 0$,则负相关。## 示例 ### 均值向量: \\ ### 协方差矩阵: \\ ```{r,fig.cap="Binary normal distribution",fig.show='hold', fig.align='center', echo=TRUE} ## 安装和加载所需的包 #install.packages("plotly") #install.packages("mvtnorm") library(plotly) library(mvtnorm) library(webshot2) # 创建网格数据 x <- seq(150, 190, length.out = 100) #身高150-190,等距的100个值 y <- seq(50, 80, length.out = 100) #体重50-80,等距的100个值 grid <- expand.grid(X = x, Y = y) #生成 x 和 y 的所有组合,用于构建一个网格数据框,以便计算多元正态分布的概率密度。 # 设置均值和协方差矩阵 mu <- c(170, 65) #设置双元正态分布的均值向量,表示均值分别为身高 170 cm 和体重 65 kg sigma <- matrix(c(100, 20, 20, 25), nrow = 2) #设置协方差矩阵,表示身高的方差为 100,体重的方差为 25,身高和体重之间的协方差为 20 # 计算概率密度 z <- dmvnorm(as.matrix(grid), mean = mu, sigma = sigma) #计算每个网格点上双元正态分布的概率密度。 # 将概率密度矩阵转换为适合绘图的形状 z_matrix <- matrix(z, nrow = 100, ncol = 100) # 绘制三维表面图 plot_ly(x = x, y = y, z = z_matrix, type = "surface") %>% layout(title = list(text = "双元正态分布的三维概率密度图", y=0.95), scene = list(xaxis = list(title = "身高 (cm)"), yaxis = list(title = "体重 (kg)"), zaxis = list(title = "概率密度"))) ``` ```{r,eval = FALSE} install.packages("webshot2") ``` `library(webshot2)` 。