生存分析
生存分析(survival analysis)是一种统计方法,用于分析时间数据, 主要研究生存时间和结局的分布及其影响因素的统计方法。在生存分析中,每个研究对象的结局变量由 “time”(生存时间) 和 “status”(生存状态)组成。生存时间是指从某个特定时间点开始,到某个事件的节点时,事件数据是指某个事件是否发生。 生存时间是一个非负实数,生存状态是一个二元变量,通常用1表示事件发生,0表示事件未发生。
生存分析的主要应用领域是医学、生物学、工程学、经济学等。
生存函数
生存函数(survival function)是生存分析的基本概念之一,它是一个函数,用于刻画研究对象在某个时刻 t 内存存活的概率。 生存函数通常用 \(S(t)\) 表示。
风险函数(hazard function)是生存分析的另一个基本概念,用于刻画研究对象在某个时刻 t 还存活但是极短的时间内死亡的风险。 风险函数通常用 \(h(t)\) 表示。
如果记寿命分布的密度为 \(f(t)\),则有: \(h(t) = f(t) / S(t)\) 。
数据集及来源
这里使用 R 语言 survival 包中的 ovarian 数据集,该数据集来自一项比较卵巢癌患者在两种治疗方式下的生存率比较的随机对照试验。
首先找到 ovarian 数据集,你可以从互联网上寻找相关资源;或者从 R 的 survival 包中导出这一数据集,操作如下:
# install.packages("survival")
library(survival)
ovarian
data(cancer, package="survival")
df <- ovarian
write.csv(df, "your-file-path\\ovarian.csv", row.names = FALSE)
将数据集下载到你的工作目录,然后使用 Pandas 导入与读取:
import pandas as pd
ovarian = pd.read_csv(r"C:\Users\asus\Desktop\R\quarto\Med-Stat-Notes\Data\ovarian.csv")
ovarian.head()
| 0 |
59 |
1 |
72.3315 |
2 |
1 |
1 |
| 1 |
115 |
1 |
74.4932 |
2 |
1 |
1 |
| 2 |
156 |
1 |
66.4658 |
2 |
1 |
2 |
| 3 |
421 |
0 |
53.3644 |
2 |
2 |
1 |
| 4 |
431 |
1 |
50.3397 |
2 |
1 |
1 |
数据集包括 26 个观测值,6 个变量。变量如下:futime(随访时间),fustat(研究结束时的状态:0 表示存活,1表示死亡),age(患者的年龄),resid.ds(疾病残留情况:1 表示有残留,2 表示没有残留),rx(治疗方式:1 表示环磷酰胺,2 表示环磷酰胺+阿霉素)和 ecog.ps(患者的 ECOG 评分:1 表示较好,2 表示较差)。
对年龄进行分组,分为 <50 和 >50 两组,并将其他三个变量的各水平加上相应的标签。
# 查看 ovarian(DataFrame)的变量名,因为不同的渠道下载的 Dataset 可能会有区别
print(ovarian.columns)
# 将 age 列转换为数值类型
ovarian['age'] = pd.to_numeric(ovarian['age'], errors='coerce')
ovarian.age = pd.cut(ovarian.age, [0,50,75], labels = ['<=50','>50'])
ovarian['resid.ds'] = ovarian['resid.ds'].map({1: "NO", 2: "Yes"})
ovarian['rx'] = ovarian['rx'].map({1: "A", 2: "B"})
ovarian['ecog.ps'] = ovarian['ecog.ps'].map({1: "Good", 2: "Bad"})
Index(['futime', 'fustat', 'age', 'resid.ds', 'rx', 'ecog.ps'], dtype='object')
生存率的 Kaplan-Meier 估计
生存率的 Kaplan-Meier 估计的计算可以调用 lifelines 库中的 KaplanMeierFitter 函数实现。
pip 安装:pip install lifelines
conda 安装: conda install lifelines
拟合 fit :
from lifelines import KaplanMeierFitter
kmf = KaplanMeierFitter()
fit = kmf.fit(ovarian.futime,ovarian.fustat)
fit
<lifelines.KaplanMeierFitter:"KM_estimate", fitted with 26 total observations, 14 right-censored observations>
拟合结果 fit 包含了很多属性,我们可以通过点操作符单独提取其中的属性。例如,查看中位生存时间:
fit.median_survival_time_
中位数生存时间表示,有 50% 的患者生存时间达到了 638 天。还可以提取寿命表和生存函数等属性,通过以下方式实现合并查看:
pd.concat([fit.event_table,fit.survival_function_], axis = 1)
| 0.0 |
0 |
0 |
0 |
26 |
26 |
1.000000 |
| 59.0 |
1 |
1 |
0 |
0 |
26 |
0.961538 |
| 115.0 |
1 |
1 |
0 |
0 |
25 |
0.923077 |
| 156.0 |
1 |
1 |
0 |
0 |
24 |
0.884615 |
| 268.0 |
1 |
1 |
0 |
0 |
23 |
0.846154 |
| 329.0 |
1 |
1 |
0 |
0 |
22 |
0.807692 |
| 353.0 |
1 |
1 |
0 |
0 |
21 |
0.769231 |
| 365.0 |
1 |
1 |
0 |
0 |
20 |
0.730769 |
| 377.0 |
1 |
0 |
1 |
0 |
19 |
0.730769 |
| 421.0 |
1 |
0 |
1 |
0 |
18 |
0.730769 |
| 431.0 |
1 |
1 |
0 |
0 |
17 |
0.687783 |
| 448.0 |
1 |
0 |
1 |
0 |
16 |
0.687783 |
| 464.0 |
1 |
1 |
0 |
0 |
15 |
0.641931 |
| 475.0 |
1 |
1 |
0 |
0 |
14 |
0.596078 |
| 477.0 |
1 |
0 |
1 |
0 |
13 |
0.596078 |
| 563.0 |
1 |
1 |
0 |
0 |
12 |
0.546405 |
| 638.0 |
1 |
1 |
0 |
0 |
11 |
0.496732 |
| 744.0 |
1 |
0 |
1 |
0 |
10 |
0.496732 |
| 769.0 |
1 |
0 |
1 |
0 |
9 |
0.496732 |
| 770.0 |
1 |
0 |
1 |
0 |
8 |
0.496732 |
| 803.0 |
1 |
0 |
1 |
0 |
7 |
0.496732 |
| 855.0 |
1 |
0 |
1 |
0 |
6 |
0.496732 |
| 1040.0 |
1 |
0 |
1 |
0 |
5 |
0.496732 |
| 1106.0 |
1 |
0 |
1 |
0 |
4 |
0.496732 |
| 1129.0 |
1 |
0 |
1 |
0 |
3 |
0.496732 |
| 1206.0 |
1 |
0 |
1 |
0 |
2 |
0.496732 |
| 1227.0 |
1 |
0 |
1 |
0 |
1 |
0.496732 |
绘制生存曲线
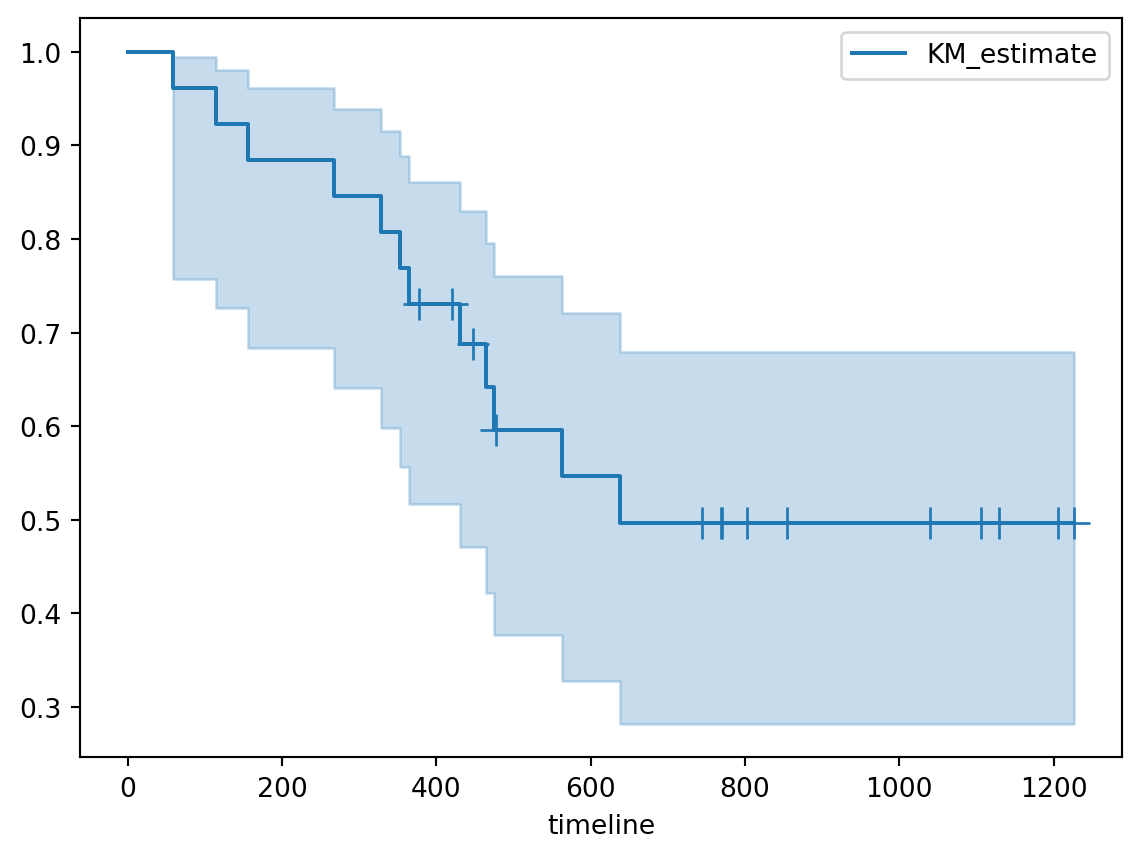
Kaplan-Meier 法估计的生存率是一个阶梯状的函数,其阶梯跳跃点是给定的时间点,我们可以通过调用 plot 方法绘制生存曲线,如图所示:
import matplotlib.pyplot as plt
fit.plot(show_censors = True)
plt.show()
生存率的比较
在生存分析中,经常需要比较不同情形下的生存率。在本例中,想要比较不同治疗方式下生存率,可以输入下面的命令:
g1 = ovarian.rx == "A"
g2 = ovarian.rx == "B"
kmf_A = KaplanMeierFitter()
kmf_A.fit(ovarian.futime[g1],ovarian.fustat[g1],label = "Treatmeat A")
kmf_B = KaplanMeierFitter()
kmf_B.fit(ovarian.futime[g2],ovarian.fustat[g2],label = "Treatmeat B")
<lifelines.KaplanMeierFitter:"Treatmeat B", fitted with 13 total observations, 8 right-censored observations>
Kaplan-Meier 比较图
可以单独提取两组的生存函数进行比较,但在同一个图中显示多条生存曲线更有助于生存率的比较。
fig, axes = plt.subplots()
kmf_A.plot(ax = axes,show_censors = True)
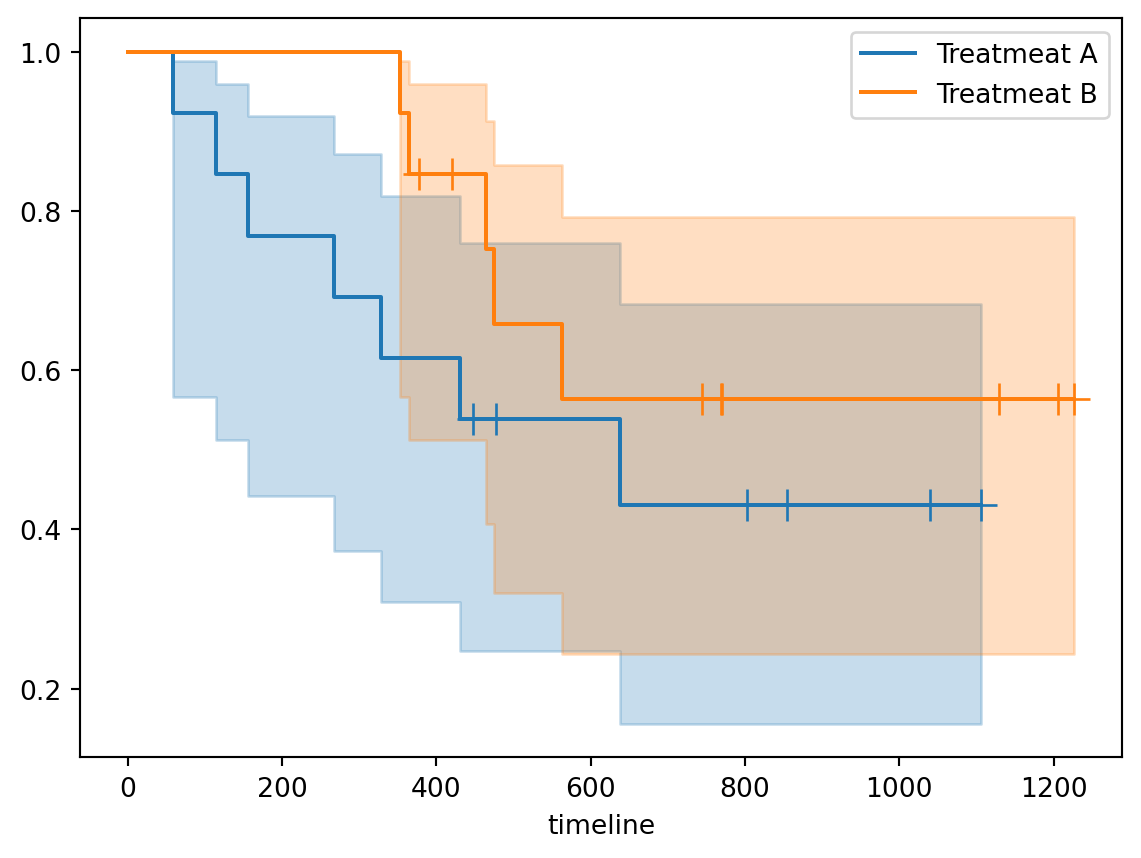
kmf_B.plot(ax = axes,show_censors = True)
plt.show()
从上图中可以看出,治疗方式 “B” 的生存率高于治疗方式 “A” 的生存率,但是这种差异是由随机误差引起还是真是的治疗方式的不同所造成的差异,需要做进一步的统计学检验。
统计学检验
生存分析中常用的统计学检验是 时序检验(log rank test),其基本思想是先计算出不同时间两种治疗方式的暴露人数和死亡人数,并由此在两种治疗方式效果相同的假设下计算出预期死亡人数,如果不拒绝零假设( \(H_0\) :两种治疗方式的效果相同,即预期死亡人数一致),则实际观测值和期望值的差异不会很大,如果差异过大则不能认为该差异是由随机误差引起的。
对此,用 \(\chi^2\) 检验做判断。时序检验可以用 lifetimes 库的函数 logrank_test 实现。
from lifelines.statistics import logrank_test
lr = logrank_test(ovarian.futime[g1], ovarian.futime[g2],
ovarian.fustat[g1], ovarian.fustat[g2])
lr.p_value
这里得到的结果为 \(P>0.05\) ,在一般情况下,我们会认为这是没有统计学意义的,即无法排除差异是由随机误差引起的。
这种结果不显著的情况下,我们可以做一些思考,即是否有其他因素干预了结果的显著性,以及是否是样本量过小,导致差异不显著。(样本量的大小会影响检验效能,如果检验效能太低,即使有差异,也很难被检验方法发现)
这里我们无法改变样本量的大小,但是可以考虑其他混杂因素的影响,并且使用更全面的模型进行检验。
Cox 回归
所有的参数回归模型需要对风险函数做出假设,这些模型可以对每个时间点的生存概率进行估计。而 Cox 回归没有关于风险函数的假设,他所遵循的唯一重要假设是 “比例风险” 。
\[
h(t,X)=h_0(t)e^{\sum{\beta_i}{X_i}}
\]
等式左边表示风险收时间和自变量的影响,等式右边的 \(h_0(t)\) 是所有自变量 \(X_i\) 都为 0 时的基线风险函数, \(e^{\sum{\beta_i}{X_i}}\) 表示所有自变量 \(X_i\) 和对应的估计系数 \(\beta_i\) 的乘积之和。
因此有:
\[
\frac{h(t,X)}{h_0(t)}=e^{\sum{\beta_i}{X_i}}
\]
建立模型
在建立模型前,需要对分类变量进行哑变量处理:
df_dummy = pd.get_dummies(ovarian,drop_first = True)
df_dummy.head()
| 0 |
59 |
1 |
True |
True |
False |
True |
| 1 |
115 |
1 |
True |
True |
False |
True |
| 2 |
156 |
1 |
True |
True |
False |
False |
| 3 |
421 |
0 |
True |
True |
True |
True |
| 4 |
431 |
1 |
True |
True |
False |
True |
使用 drop_first = True 参数是为了去掉各个参考类别。
下面将所有的协变量都纳入,建立 Cox 回归模型:
from lifelines import CoxPHFitter
cox = CoxPHFitter()
cox.fit(df_dummy,duration_col = 'futime', event_col = 'fustat')
cox.print_summary()
| model |
lifelines.CoxPHFitter |
| duration col |
'futime' |
| event col |
'fustat' |
| baseline estimation |
breslow |
| number of observations |
26 |
| number of events observed |
12 |
| partial log-likelihood |
-28.89 |
| time fit was run |
2025-08-03 06:50:54 UTC |
| age_>50 |
2.20 |
9.04 |
1.11 |
0.03 |
4.37 |
1.03 |
79.10 |
0.00 |
1.99 |
0.05 |
4.42 |
| resid.ds_Yes |
1.45 |
4.25 |
0.73 |
0.02 |
2.88 |
1.02 |
17.75 |
0.00 |
1.98 |
0.05 |
4.40 |
| rx_B |
-1.38 |
0.25 |
0.64 |
-2.65 |
-0.12 |
0.07 |
0.89 |
0.00 |
-2.14 |
0.03 |
4.96 |
| ecog.ps_Good |
-0.59 |
0.56 |
0.63 |
-1.83 |
0.65 |
0.16 |
1.92 |
0.00 |
-0.93 |
0.35 |
1.50 |
| Concordance |
0.79 |
| Partial AIC |
65.78 |
| log-likelihood ratio test |
12.19 on 4 df |
| -log2(p) of ll-ratio test |
5.97 |
结果显示,在调整了协变量后,两种治疗方式的死亡风险的差异具有统计学意义(P<0.05)。
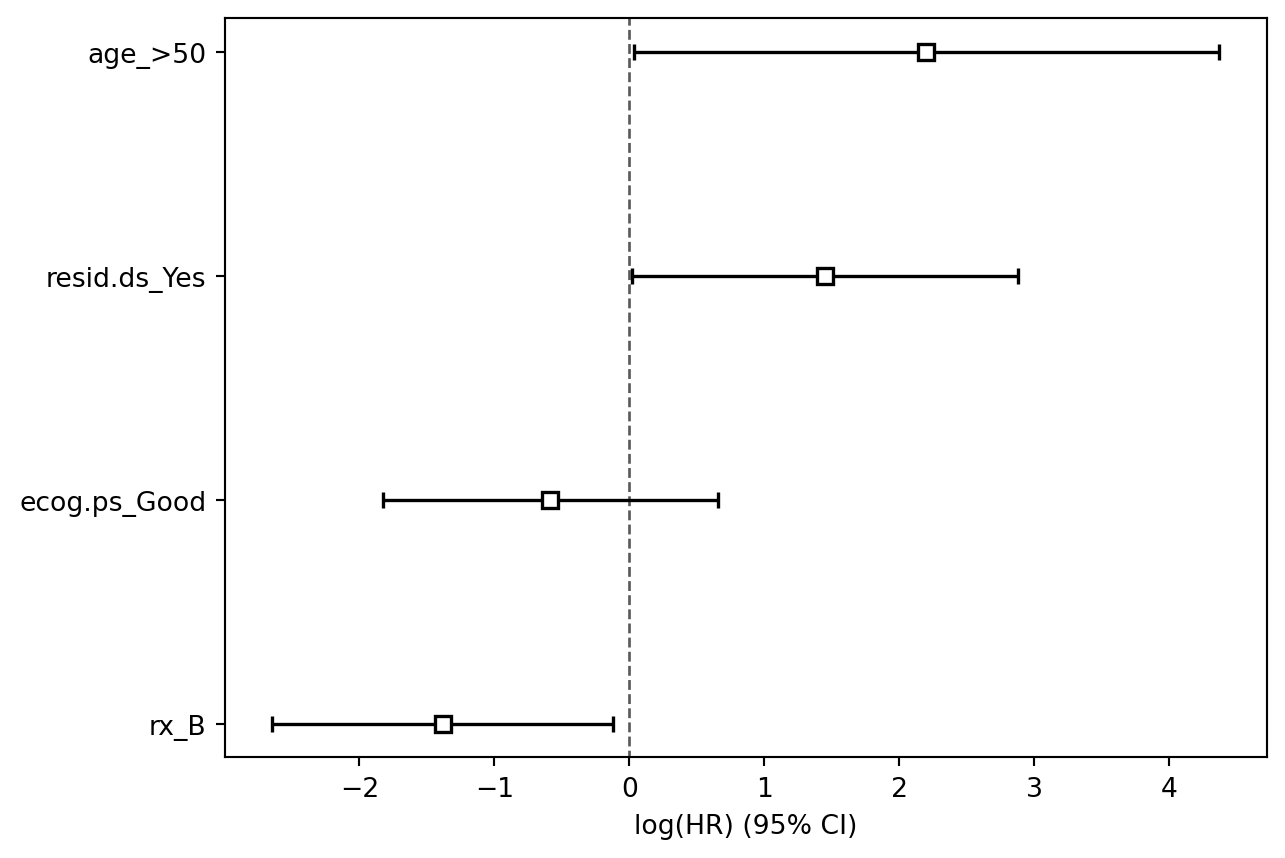
模型的回归系数及其置信区间可以通过 plot 方法进行直观展示:
Cox 回归是一种半参数回归模型,也像多元线性回归一样,存在变量选择的问题。通常可以用 AIC 进行变量选择。
查看当前模型的 AIC 值:
根据前序的结果,变量 ecog.ps 对应的 P 值最大,对其进行剔除后再次拟合模型:
cox1 = CoxPHFitter()
df_dummy_sub = df_dummy.drop('ecog.ps_Good', axis = 1)
cox1.fit(df_dummy_sub, duration_col = 'futime', event_col = 'fustat')
cox1.print_summary()
cox1.AIC_partial_
| model |
lifelines.CoxPHFitter |
| duration col |
'futime' |
| event col |
'fustat' |
| baseline estimation |
breslow |
| number of observations |
26 |
| number of events observed |
12 |
| partial log-likelihood |
-29.33 |
| time fit was run |
2025-08-03 06:50:55 UTC |
| age_>50 |
2.11 |
8.29 |
1.09 |
-0.02 |
4.25 |
0.98 |
70.32 |
0.00 |
1.94 |
0.05 |
4.25 |
| resid.ds_Yes |
1.25 |
3.50 |
0.69 |
-0.10 |
2.61 |
0.90 |
13.58 |
0.00 |
1.81 |
0.07 |
3.83 |
| rx_B |
-1.28 |
0.28 |
0.62 |
-2.50 |
-0.06 |
0.08 |
0.94 |
0.00 |
-2.06 |
0.04 |
4.67 |
| Concordance |
0.77 |
| Partial AIC |
64.66 |
| log-likelihood ratio test |
11.31 on 3 df |
| -log2(p) of ll-ratio test |
6.62 |
剔除 ecog_ps 后的模型, AIC 值有所下降,但是不多(谨慎对待),能认为新模型优于原有模型。