DID 双重差分模型
1 DID 双重差分模型
1.1 DID 定义与目标
双重差分回归 (DID) 用于评估一个事件的因果效应,其方法是比较事件发生的单元集合(处理组)与事件未发生的单元集合(控制组)。
DID 背后的逻辑是,如果事件从未发生,处理组和控制组之间的差异应该随着时间的推移保持不变。
DID 通过比较处理组和控制组在事件发生前后的差异来估计事件的因果效应。
DID 法是一种无法随机分配样本情况下的替代方法,主要应用于区域行的策略评估问题。
目标:获取相对同质的策略组和控制组,这个“相对”是指除策略影响外,策略组和控制组的结果变量随时间的变化存在一个基本固定的差异。
对于相对同质的策略组和控制组,DID法通过第一次的差分消除这个基本固定的差异,通过第二次的差分消除时间趋势的影响,评估策略带来的实际效应。
从DID 法的目标中可知,该方法面对的实验数据是面板数据(多个时间点的截面数据组成面板数据),即在策略干预时间点前,至少有两个时间点的数据。
1.2 DID 模型的原理
1.2.1 DID 模型公式化表现
\[ y = \alpha_0 +\alpha_1g +\alpha_2T + \alpha_3gT + \epsilon \]
其中,\(\alpha_0\)为常数项,\(\alpha_1\)为处理组和控制组的差异,\(\alpha_2\)为时间效应,\(\epsilon\)为误差项。
\(y\)为结果变量,\(g\)为处理组和控制组的虚拟变量,\(T\)为时间虚拟变量,\(gT\)为交互项。
\(\alpha_3\)为交互项的系数,也就是DID的估计量,当交互项 \(gT\) 与结果变量 \(y\) 显著相关时,\(\alpha_3\) 为评估的实际的策略效应,表示处理组和控制组在事件发生前后的差异。
1.2.2 DID模型示意图
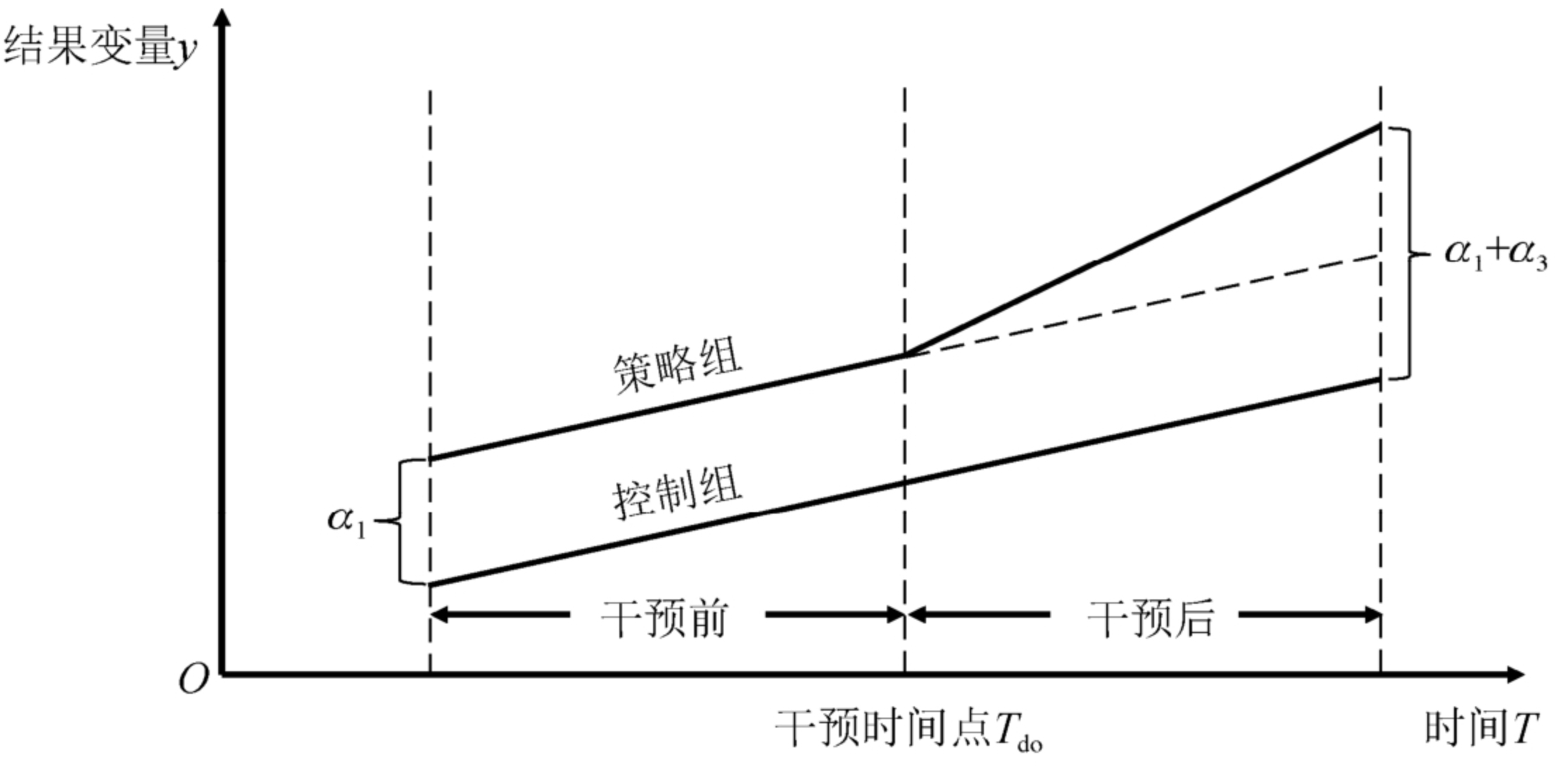
1.2.3 DID模型的回归系数关于组别和干预时间段的二联表
| 组别 | 干预前(T=0) | 干预后(T=1) | 差分(干预后非策略差异) |
|---|---|---|---|
| 策略组(g=1) | \(\alpha_0+\alpha_1\) | \(\alpha_0+\alpha_1+\alpha_2+\alpha_3\) | \(\alpha_2+\alpha_3\) |
| 控制组(g=0) | \(\alpha_0\)(基准值) | \(\alpha_0+\alpha_2\) | \(\alpha_2\) |
| 差分(组间差异) | \(\alpha_1\) | \(\alpha_1+\alpha_3\) | \(\alpha_3\)(策略效应) |
DID模型的原理很清晰,在无法获取完全同质的策略组和控制组的情况下,替代地获取存在固定组间差异的试验数据以抵抗混杂的影响,最后通过回归系数的显著性检验来评估策略实施的净效应。但是,理论很简洁,现实很残酷,获取 @ref(DID-models) 所示的理想数据并不简单,为了保证DID模型可以有效地评估策略效应,需要一些必要的前提检验。下面介绍这些关于DID模型的有效性检验。
1.3 DID 模型的有效性检验
为了保证该模型的有效性,在试验设计时需要满足平行趋势假设:在事件发生前,处理组和控制组的结果变量随时间的变化存在一个基本固定的差异。
平行趋势,即策略组和控制组在干预前保持相同的变化趋势。
3种常见的平行趋势的检验方法:
画图法:画出处理组和控制组在事件发生前后的结果变量的变化趋势图,观察两组的变化趋势是否平行。
统计检验法(差异性检验):使用t检验或F检验等统计方法,检验处理组和控制组在事件发生前的结果变量的差异是否显著。
伪DID法(交互项显著性检验):在事件发生前,随机选择一个时间点,将处理组和控制组的结果变量进行差分,检验差分后的结果变量是否显著。
1.4 DID 案例分析
数据来自 princeton 的 Oscar Torres-Reyna 教授构建的虚拟数据集。
案例数据示例如下表所示: